The vertices of a regular hexagon lie on a circle with centre O and radius 5 cm. AQA GCSE 8300/1H

AQA GCSE 8300/1H
Question: The vertices of a regular hexagon lie on a circle with centre O and radius 5 cm.

Work out the shaded area.
Give your answer in the form a

where a, b and c are integers.

Explanation: To find the area first we need to denote the figure with point names.

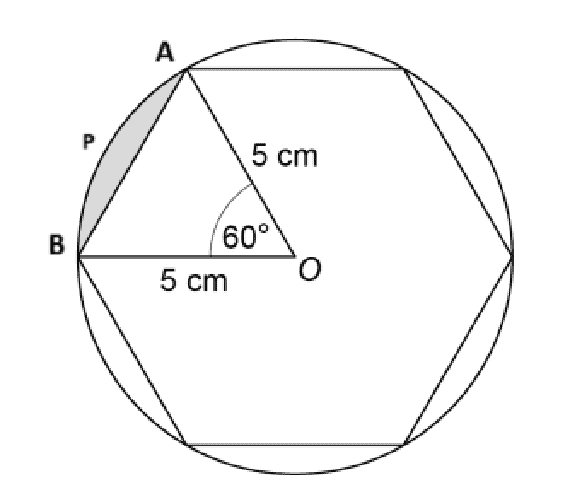
To get the area of shaded region we need to subtract the area of ABO from area of APBO

Area of region ABO:

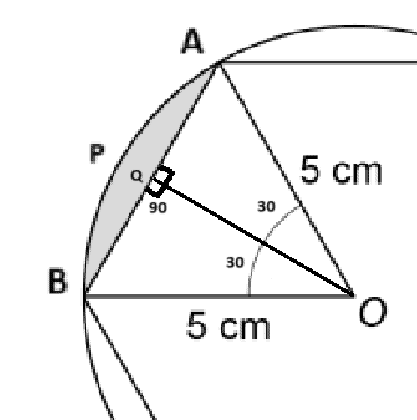
side BQ = OB*sin(30)
= 5*1/2
side AB = 2*BQ = 5
side OQ = 5*cos(30)
= 5*√3/2
Area ABO = 1/2 * AB * OQ
= 1/2 * 5 * 5*√3/2
= 25√3/4

Area of region APBO:
Area = θ/360 * πr²
= 60/360 * π*25
= 25π/6

Subtracting area ABO from area APBO
we get,
required area = 25π/6 – 25√3/4
= (25*2π – 25*3√3)/12
= (50π – 75√3)/12

which is of the given form.
Hence, (50π – 75√3)/12 is the required area.

AQA GCSE 8300/1H Solution

if you want to sharp your brain and for daily GCSE Maths questions just follow @reasoningwizard on Instagram
To Get Solutions of Past year AQA GCSE visit here.