Best Questions of AQA GCSE Mathematics 83002H June 2022

Table of Contents

AQA GCSE June 2022
Q3: Circle the triangular number.
9 12 15 18

Ans: A triangular number is a number that can be represented as a triangle with dots. The formula for the nth triangular number is given by Tn=n×(n+1)/2.

Let’s check which of the numbers 9, 12, 15, and 18 are triangular numbers:

For n=3, T3=23×(3+1)=6
For n=4, T4=24×(4+1)=10
For n=5, T5=25×(5+1)=15
For n=6, T6=26×(6+1)=21

So, 9 is not a triangular number, 12 is not a triangular number, 15 is a triangular number, and 18 is not a triangular number. Therefore, the triangular number in the list is 15.

Q6: Show that 2125 can be written as
a cube number multiplied by a prime number between 10 and 20.

AQA GCSE June 2022
Ans: To show that 2125 can be written as a cube number multiplied by a prime number between 10 and 20, let’s factorize 2125.

2125=5×5×5×172125=5×5×5×17

Now, we can express 2125 as a cube number (5 cubed) multiplied by a prime number (17):

2125=(5)³×172125=(5)³×17

So, 2125 can be written as the cube of 5 (a cube number) multiplied by 17 (a prime number between 10 and 20).

83002H
Q7: Sam types a constant number of words per minute.
He takes 8 minutes to type a report of 416 words.
How long does it take him to type an essay of 1534 words?
Give your answer in minutes and seconds.

AQA GCSE June 2022
Ans: Let’s denote the constant number of words Sam types per minute as W.

In the first scenario, Sam types a report of 416 words in 8 minutes. So, his typing speed is 416/8=52 words per minute.

Now, we can use this information to find how long it takes him to type an essay of 1534 words.

The time (in minutes) it takes him to type the essay is given by Number of words in the essay/Words typed per minuteWords typed per minuteNumber of words in the essay:

Time (minutes)=1534/52≈29.5 minutes

Now, to convert the decimal part of the minutes to seconds, we can use the fact that there are 60 seconds in a minute.

0.5minutes=0.5×60=30seconds

So, it takes Sam approximately 29 minutes and 30 seconds to type an essay of 1534 words.

83002H
Q8: A school play takes place each day from Monday to Friday.
Here are the attendances on four of the days.
Monday Tuesday Wednesday Thursday
72 83 88 97
For all five days, the mean attendance is 90
Work out the attendance on Friday.

AQA GCSE June 2022
Ans: To find the attendance on Friday, we can use the mean attendance formula:

Mean = (Sum of all values) / (Number of values)

Given that the mean attendance for all five days is 90, and the attendances for Monday, Tuesday, Wednesday, and Thursday are provided, we can calculate the total attendance for all five days.

Let A be the attendance on Friday.

The sum of all five days’ attendance is 72+83+88+97+A, and the number of values is 5.

So, we have the equation:

90=(72+83+88+97+A)/5

Now, solve for A:

90×5=72+83+88+97+A

450=340+A

A=450−340

A=110

Therefore, the attendance on Friday is 110.

83002H
Q9: Rosie makes phone calls to try to sell broadband.
Today, she made 120 calls.
The table shows the results.

Result of call Frequency
Not answered 33
Answered but sale not made 81
Answered and sale made 6
(a) Write down the relative frequency that a call was not answered.

AQA GCSE June 2022
Ans:

The relative frequency of a particular outcome is calculated by dividing the frequency of that outcome by the total number of trials (in this case, the total number of calls).

For the result “Not answered,” the frequency is 33. The total number of calls made is 120.

The relative frequency (RF) for “Not answered” is given by:

RF=Frequency of Not answered/Total number of calls

Substitute the values:

RF=33/120

Now, simplify the fraction if possible:

RF=11/40

So, the relative frequency that a call was not answered is 11/40.

(b) During the rest of the week, Rosie will make 500 calls.
Using the results in the table, how many sales does she expect to make during the
rest of the week?

AQA GCSE June 2022
Ans: To estimate the number of sales Rosie expects to make during the rest of the week, we can use the relative frequency of making a sale from the given results.

The relative frequency of making a sale is calculated by dividing the frequency of “Answered and sale made” by the total number of calls.

Given:

Frequency of “Answered and sale made” = 6
Total number of calls made today = 120

Relative frequency (RF) for making a sale is given by:

RF=Frequency of Answered and sale made/Total number of calls

Substitute the values:

RF=6/120

Now, simplify the fraction if possible:

RF=1/20

Now, apply this relative frequency to the rest of the week. Rosie will make 500 calls, so the expected number of sales (E) during the rest of the week is given by:

E=RF×Total number of calls during the rest of the week

E=1/20×500

Now, calculate:

E=500/20

E=25

Therefore, Rosie expects to make approximately 25 sales during the rest of the week.

83002H
Q10:Harry and Ellie each bought a printer and a hard drive.
Here is some information about how much they paid
Printer Hard drive
Harry £80 £25
Ellie 10% less than Harry 20% more than Harry
Ellie says,
‘‘In total, I paid more than Harry because 20% is greater than 10%’’
Is she correct?
Tick a box.
Show calculations to support your answer.

AQA GCSE June 2022
Ans: Let’s calculate the cost of the printer and hard drive for both Harry and Ellie.

For Harry:

Printer cost: £80
Hard drive cost: £25

For Ellie:

Ellie pays 10% less than Harry for the printer.
- 10% of £80 = 0.10×80=£80.10×80=£8
- Ellie’s printer cost: £80 – £8 = £72
Ellie pays 20% more than Harry for the hard drive.
- 20% of £25 = 0.20×25=£50.20×25=£5
- Ellie’s hard drive cost: £25 + £5 = £30

Now, let’s find the total cost for both Harry and Ellie:

Harry’s total cost: £80 (printer) + £25 (hard drive) = £105
Ellie’s total cost: £72 (printer) + £30 (hard drive) = £102

Ellie claims that she paid more than Harry because 20% is greater than 10%. Let’s check if this is true:

Ellie paid £102, and Harry paid £105.

The percentage difference between their total costs is given by:

Percentage difference=((Ellie’s cost – Harry’s cost)/Harry’s cost)×100

Substitute the values:

Percentage difference=((102−105)/105)×100≈−2.86%

The negative sign indicates that Ellie paid less than Harry, not more. Therefore, Ellie is not correct; she did not pay more than Harry.

83002H
Q11:A shape is made by joining a right-angled triangle to a rectangle.
Work out the area of the shape.

AQA GCSE June 2022
Ans: Area of the shape = Area of Triangle + Area of Rectangle

Area of Triangle = 1/2 * base * height

= 1/2 * 16 * 30

= 240

Area of Rectangle = Base * Height

= (34)(using pythagoras theorem) * 52

= 1768

Area of Shape = 1768 + 240

= 2008

Hence, Area of the given shape is 2008 sq. unit.

83002H
Q13: Outside a cafe there is a large plastic ice cream cornet.
The cornet is a hemisphere on top of a cone.

The cone and the hemisphere each have radius 24 cm
The cone has perpendicular height 117 cm
(a)Work out the total volume of the cornet.

AQA GCSE June 2022
Ans: To find the total volume of the cornet, we need to find the volumes of the cone and the hemisphere separately and then add them.

The formula for the volume of a cone is given by:

Vcone=1/3 * πr²h

where r is the radius and ℎ is the perpendicular height.

The formula for the volume of a hemisphere is given by:

Vhemisphere=2/3 * πr³

In this case, the radius (r) for both the cone and the hemisphere is 24 cm.

For the cone: Vcone=1/3 * π(24²)(117)

For the hemisphere: Vhemisphere=2/3 * π(24³)

Now, add the volumes of the cone and the hemisphere to find the total volume (Vtotal):

Vtotal=Vcone+Vhemisphere

Vtotal= 70,536.96 + 28,938.24

Now, the total volume of the cornet is 99,475.2 sq cm.

(b) The actual cornets that the cafe sells are similar to the plastic one.
For the actual cornets, the cone and the hemisphere each have radius 2 cm
How many times greater is the volume of the plastic cornet than an actual cornet?

AQA GCSE June 2022
Ans: The volume V of a cone is given by the formula:

Vcone=1/3π(rcone)²(hcone)

The volume V of a hemisphere is given by the formula:

Vhemisphere=2/3π(rhemisphere)³

For the actual cornet with both a cone and a hemisphere, the total volume Vtotal is the sum of the volumes of the cone and the hemisphere:

Vtotal=Vcone+Vhemisphere

Now, we’re that the radii for both the cone and the hemisphere of the actual cornet are 2 cm.

Let’s substitute rcone=rhemisphere=2 into the volume formulas:

Vtotal=1/3π(2)²(117) + 2/3π(2)³

= 490.08 + 16.7551

= 506.5867

After taking the ratio of both volumes we get that the previous volume is approx 196 times bigger the current volume.

83002H
Q14: A survey was held in a football stadium.
A sample of the crowd was asked about the importance of a family area.
The pie chart represents the answers.

(a) The total number of people in the crowd was 29250
Estimate how many people in the crowd think that a family area is very important.
Assume that the sample is representative of the crowd.

AQA GCSE June 2022
Ans: To estimate how many people in the crowd think that a family area is very important, we can use the proportions from the survey sample.

First, calculate the total number of people who responded to the survey:

375(not important)+400(quite important)+1475(very important)=2250

Now, find the proportion of people who think a family area is very important:

Proportion of very important=1475/2250

Now, apply this proportion to the total number of people in the crowd (29250):

Estimated number of people who think it’s very important=Proportion of very important×Total crowd

Estimated number=1475/2250×29250

Now, calculate this value:

Estimated number=1475/2250×29250≈19175

Therefore, an estimated 19,175 people in the crowd think that a family area is very important.

(b) In fact, 50% of the sample were sitting in the family area 10% of the crowd were sitting in the family area. What is this likely to mean about the actual number of people in the crowd who think that a family area is very important?
Tick one box.
It is larger than the answer to part (a)
It is the same as the answer to part (a)
It is lower than the answer to part (a)

AQA GCSE June 2022
Ans: Given that 50% of the sample were sitting in the family area and only 10% of the crowd were sitting in the family area, it suggests that the sample is not representative of the entire crowd. The people who were surveyed were disproportionately from the family area, leading to an overestimation of the importance of the family area based on the survey.

Therefore, the actual number of people in the crowd who think that a family area is very important is likely lower than the answer to part (a). Tick the box that says “It is lower than the answer to part (a).”

83002H
Q15: In the grid, the product of each row, column and diagonal is 1
Complete the grid.

AQA GCSE June 2022
Ans:

83002H
Q16: Amol owns a sandwich shop.
The shop is open from Monday to Saturday.
In June, Amol sold 3000 sandwiches.
(a) Amol wants to work out the mean number of sandwiches he sold per day in June.
His method is 3000 ÷ 30 = 100
Make one criticism of Amol’s method.

AQA GCSE June 2022
Ans: Amol’s method of calculating the mean number of sandwiches sold per day (3000 ÷ 30 = 100) assumes that each month has 30 days. However, June doesn’t always have 30 days; it can have 30 or 31 days, depending on the year.

To calculate the mean accurately, Amol should have divided the total number of sandwiches sold (3000) by the actual number of days in June. This would provide a more precise measure of the average sandwiches sold per day.

(b) Amol received £6660 from selling the 3000 sandwiches in June. The numbers of sandwiches sold were in the ratio meat : cheese : vegan = 9 : 4 : 7 The price of a meat sandwich is £2.39 The price of a cheese sandwich is £1.89 Work out the price of a vegan sandwich.

AQA GCSE June 2022
Ans: Let the numbers of meat, cheese, vegan sandwiches sold be 9x, 4x, 7x

then, Total number of sandwich: 20x = 3000
x = 150

No. of meat sandwich = 9*150 = 1350
No. of cheese sandwich = 4*150 = 600
No. of vegan sandwich = 7*150 = 1050

Price of meat sandwich = £2.39 * 1350 = £3226.5
Price of cheese sandwich = £1.89 * 600 = £1134

Price of vegan sandwich = £6660-(£3226.5+£1134) = 2299.5
Price of 1 vegan sandwich = £2299.5/£1050 = £2.19

Hence, the price of one vegan sandwich = £2.19

83002H
Q20: A company makes and sells boxes of washing powder.
The company wants to increase the amount of money it receives per kg of powder.
To get the required increase it can
increase the price to £5.88
or
reduce the mass of powder in the box by x%
Work out the value of x to 2 decimal places.

AQA GCSE June 2022
Ans: Let’s denote the original mass of the washing powder in the box as M (in kg). The original price is £5.60 for 1.68 kg, so the price per kg is:

Original price per kg=Original price/Original mass=5.601.68 £/kg

Now, the company wants to increase the amount of money it receives per kg of powder.

Increasing the price: If the price is increased to £5.88, the new price per kg becomes:
New price per kg=New price/Original mass=5.881.68 £/kg
Reducing the mass of powder by x%: If the mass is reduced by x%, the new mass becomes M−x/100×M, and the new price per kg becomes:
New price per kg=Original price/New mass=5.60/(1−x/100)×1.68 £/kg

Now, we want the new price per kg to be equal in both cases:

5.88/1.68=5.60/((1−x/100)×1.68)

We can solve this equation to find the value of x:

5.88/1.68=5.60/((1−x/100)×1.68)

Cross-multiply to get rid of the fractions:

5.88×(1.68−0.0168x)=5.60×1.68

Solve for x:

9.8784−0.098784x=9.408

−0.098784x=−0.4704

x = 4.76

So, reducing the mass of the powder in the box by approximately 4.76% would give the company the same increase in revenue per kg as increasing the price to £5.88.

83002H
Q24: A straight line
is perpendicular to the straight line through (2, 8) and (6, 15)
and
passes through (0, 9) and (x, 17)
Work out the value of x.

AQA GCSE June 2022
Ans: To find the equation of the line passing through (2, 8) and (6, 15), you first need to determine the slope (gradient) of that line. The slope (m) of a line passing through two points )(x1,y1) and (x2,y2) is given by:

m=(y2−y1)/(x2−x1)

For the points (2, 8) and (6, 15):

m=(15−8)/(6−2)=7/4

Now, since the line you’re looking for is perpendicular to this line, the slope of the perpendicular line (m perpendicular) is the negative reciprocal of the slope you just found:

mperpendicular=−1/m=−4/7

Now, you have the slope (mperpendicular=−4/7) and a point (0,9) through which the line passes. You can use the point-slope form of a linear equation to find the equation of the line:

y−y1=mperpendicular(x−x1)

For the point ((0,9):

y−9=−4/7(x−0)

Simplify:

y−9=−4/7x

Now, you know that the line also passes through (x,17). Substitute this point into the equation:

17−9=−4/7x

Solve for x:

8=−4/7x

Multiply both sides by −7/4 to isolate x:

x=−7/4×8=−14

So, the value of x is -14.

83002H
Q25: f(x) = 2x + 5
Show that 3f(x) – 12f^-1(x) simplifies to an integer

AQA GCSE June 2022
Ans: Let’s break down the expression 3f(x)−12f^-1(x) using the given function f(x)=2x+5.

Find f^-1(x): To find the inverse function, switch f(x) and x and solve for x: y=2x+5
x=2y+5
2y=x−5
y=21(x−5)
So, f^-1(x)=21(x−5).
Substitute f(x) and f^-1(x) into the expression: 3f(x)−12f^-1(x)=3(2x+5)−12(21(x−5))
Simplify the expression: 6x+15−6(x−5)
Distribute the -6 inside the parentheses: 6x+15−6x+30
Combine like terms: 45

So, 3f(x)−12f^-1(x) simplifies to 45, which is an integer.

83002H
Q26: Two objects, J and K, are applying pressure to areas of ground.
For J, the force is 18.9 newtons and the area is 0.45 m2
pressure for J : pressure for K = 7 : 8
area for J : area for K = 9 : 5
Work out the force for K

AQA GCSE June 2022
Ans: Let’s denote the force applied by J as FJ, the area for J as AJ, the force applied by K as FK, and the area for K as AK.

According to the given information: Pressure for J/Pressure for K=(FJ/AJ)/(FK/AK)=7/8

We are also given that: Area for J/Area for K=9/5

Now, let’s express FJ in terms of FK using the pressure ratio: FJ/AJ=7/8⋅FK/AK

Given that FJ=18.9N and AJ=0.45m2, we can substitute these values into the equation above and solve for FK:

18.9/0.45=7/8⋅FK/AK

Now, let’s find the value of AK using the area ratio: AJ/AK=9/5

0.45/AK=9/5

Solving for AK: AK=0.45/(9/5)=0.25 m2

Now, substitute AK back into the pressure ratio equation:
18.9/0.45=(7/8)⋅(FK/0.25)

Now, solve for FK: =18.9⋅0.25⋅8 / (0.45⋅7)

FK≈12N

So, the force for K is approximately 12 newtons.

83002H
Q27: To be rented, a bedroom must have a floor area of at least 6.51 m2
A bedroom has a rectangular floor.
The floor measures 2.4m by 2.9 m, each correct to 2 significant figures.
Show that the bedroom can be rented.

AQA GCSE June 2022
Ans: To determine if the bedroom can be rented, we need to calculate its floor area and compare it to the minimum requirement of 6.51 m².

The formula for the area (A) of a rectangle is given by: A=length×width

Given that the length is 2.4 m and the width is 2.9 m, substitute these values into the formula: A=2.4m×2.9m

A=6.96m²

The calculated floor area is 6.96 m². Since this is greater than the minimum requirement of 6.51 m², the bedroom can be rented according to the specified condition.

83002H
Q28: AB, BC and CD are sides of a regular 12-sided polygon.
CDMN is a square.
Prove that points A, B and N lie on a straight line.

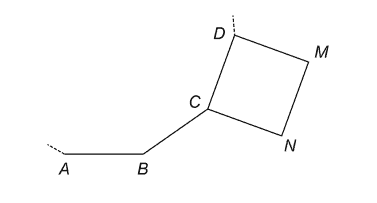
AQA GCSE June 2022
Ans: Since Angle DCB = 180 – 360/12 = 150

We are given that Angle DCN is 90.
Therefore Angle BCN = 360 – (150+90) = 120
Now, since side BC = CN
angle CBN = angle CNB
Hence angle CBN = (180 – 120)/2
= 30

Now, angle ABC = 150 and angle CBN = 30
They both sum up to 180
Hence we can say that A, B, N lie on a straight line.

83002H
Q29: The equation of a curve is y = x2 – 18x + 70
By completing the square, work out the coordinates of the turning point.
You must show your working.

AQA GCSE June 2022
Ans: To find the coordinates of the turning point of the quadratic curve y=x²−18x+70 by completing the square, follow these steps:

Write the quadratic in the form y=a(x−h)²+k: y=x²−18x+70
Factor out the coefficient of x² from the x² and x terms: �=y=(x²−18x)+70
Complete the square inside the parentheses. To do this, take half of the coefficient of x and square it. Add and subtract this value inside the parentheses: y=(x²−18x+81−81)+70
The added 81 is (−18/2)², which completes the square.
Group the perfect square trinomial and the constant term: y=(x2−18x+81)−81+70
Simplify the expression: y=(x−9)2−11
Now, the equation is in the desired form y=a(x−h)²+k, where (h,k) is the turning point of the parabola.
Identify the coordinates of the turning point: The turning point is (h,k)=(9,−11).

So, by completing the square, the coordinates of the turning point are (9,−11).

if you want to sharp your brain and for daily GCSE Maths questions just follow @learn.dayly on Instagram

Our Other Posts

Best Questions Of AQA GCSE Mathematics – Paper 2: 83002H Higher Tier Non-Calculator June 2022

AQA GCSE June 2022
Q3: Circle the triangular number.
9 12 15 18

Q6: Show that 2125 can be written as
a cube number multiplied by a prime number between 10 and 20.

83002H
Q7: Sam types a constant number of words per minute.
He takes 8 minutes to type a report of 416 words.
How long does it take him to type an essay of 1534 words?
Give your answer in minutes and seconds.

83002H
Q8: A school play takes place each day from Monday to Friday.
Here are the attendances on four of the days.
Monday Tuesday Wednesday Thursday
72 83 88 97
For all five days, the mean attendance is 90
Work out the attendance on Friday.

83002H
Q9: Rosie makes phone calls to try to sell broadband.
Today, she made 120 calls.
The table shows the results.

Result of call Frequency
Not answered 33
Answered but sale not made 81
Answered and sale made 6
(a) Write down the relative frequency that a call was not answered.

83002H
Q11:A shape is made by joining a right-angled triangle to a rectangle.
Work out the area of the shape.

83002H
Q13: Outside a cafe there is a large plastic ice cream cornet.
The cornet is a hemisphere on top of a cone.

83002H
Q14: A survey was held in a football stadium.
A sample of the crowd was asked about the importance of a family area.
The pie chart represents the answers.

83002H
Q15: In the grid, the product of each row, column and diagonal is 1
Complete the grid.

83002H
Q16: Amol owns a sandwich shop.
The shop is open from Monday to Saturday.
In June, Amol sold 3000 sandwiches.
(a) Amol wants to work out the mean number of sandwiches he sold per day in June.
His method is 3000 ÷ 30 = 100
Make one criticism of Amol’s method.

83002H
Q20: A company makes and sells boxes of washing powder.
The company wants to increase the amount of money it receives per kg of powder.
To get the required increase it can
increase the price to £5.88
or
reduce the mass of powder in the box by x%
Work out the value of x to 2 decimal places.

83002H
Q24: A straight line
is perpendicular to the straight line through (2, 8) and (6, 15)
and
passes through (0, 9) and (x, 17)
Work out the value of x.

83002H
Q25: f(x) = 2x + 5
Show that 3f(x) – 12f^-1(x) simplifies to an integer

83002H
Q26: Two objects, J and K, are applying pressure to areas of ground.
For J, the force is 18.9 newtons and the area is 0.45 m2
pressure for J : pressure for K = 7 : 8
area for J : area for K = 9 : 5
Work out the force for K

83002H
Q27: To be rented, a bedroom must have a floor area of at least 6.51 m2
A bedroom has a rectangular floor.
The floor measures 2.4m by 2.9 m, each correct to 2 significant figures.
Show that the bedroom can be rented.

83002H
Q28: AB, BC and CD are sides of a regular 12-sided polygon.
CDMN is a square.
Prove that points A, B and N lie on a straight line.

83002H
Q29: The equation of a curve is y = x2 – 18x + 70
By completing the square, work out the coordinates of the turning point.
You must show your working.

if you want to sharp your brain and for daily GCSE Maths questions just follow @learn.dayly on Instagram

1 thought on “Best Questions Of AQA GCSE Mathematics – Paper 2: 83002H Higher Tier Non-Calculator June 2022”

AQA GCSE June 2022Q3: Circle the triangular number. 9 12 15 18

Q6: Show that 2125 can be written asa cube number multiplied by a prime number between 10 and 20.

83002HQ7: Sam types a constant number of words per minute.He takes 8 minutes to type a report of 416 words.How long does it take him to type an essay of 1534 words?Give your answer in minutes and seconds.

83002HQ8: A school play takes place each day from Monday to Friday.Here are the attendances on four of the days. Monday Tuesday Wednesday Thursday 72 83 88 97For all five days, the mean attendance is 90Work out the attendance on Friday.

83002HQ9: Rosie makes phone calls to try to sell broadband.Today, she made 120 calls.The table shows the results.Result of call FrequencyNot answered 33Answered but sale not made 81Answered and sale made 6(a) Write down the relative frequency that a call was not answered.

83002HQ11:A shape is made by joining a right-angled triangle to a rectangle.Work out the area of the shape.

83002HQ13: Outside a cafe there is a large plastic ice cream cornet.The cornet is a hemisphere on top of a cone.

83002HQ14: A survey was held in a football stadium.A sample of the crowd was asked about the importance of a family area.The pie chart represents the answers.

83002HQ15: In the grid, the product of each row, column and diagonal is 1Complete the grid.

83002HQ16: Amol owns a sandwich shop.The shop is open from Monday to Saturday.In June, Amol sold 3000 sandwiches.(a) Amol wants to work out the mean number of sandwiches he sold per day in June.His method is 3000 ÷ 30 = 100Make one criticism of Amol’s method.

83002HQ20: A company makes and sells boxes of washing powder.The company wants to increase the amount of money it receives per kg of powder.To get the required increase it canincrease the price to £5.88orreduce the mass of powder in the box by x%Work out the value of x to 2 decimal places.

83002HQ24: A straight lineis perpendicular to the straight line through (2, 8) and (6, 15)andpasses through (0, 9) and (x, 17)Work out the value of x.

83002HQ25: f(x) = 2x + 5Show that 3f(x) – 12f-1(x) simplifies to an integer

83002HQ26: Two objects, J and K, are applying pressure to areas of ground.For J, the force is 18.9 newtons and the area is 0.45 m2pressure for J : pressure for K = 7 : 8area for J : area for K = 9 : 5Work out the force for K

83002HQ27: To be rented, a bedroom must have a floor area of at least 6.51 m2A bedroom has a rectangular floor.The floor measures 2.4m by 2.9 m, each correct to 2 significant figures.Show that the bedroom can be rented.

83002HQ28: AB, BC and CD are sides of a regular 12-sided polygon.CDMN is a square.Prove that points A, B and N lie on a straight line.

83002HQ29: The equation of a curve is y = x2 – 18x + 70By completing the square, work out the coordinates of the turning point.You must show your working.

if you want to sharp your brain and for daily GCSE Maths questions just follow @learn.dayly on Instagram

1 thought on “Best Questions Of AQA GCSE Mathematics – Paper 2: 83002H Higher Tier Non-Calculator June 2022”

AQA GCSE June 2022
Q3: Circle the triangular number.
9 12 15 18

Q6: Show that 2125 can be written as
a cube number multiplied by a prime number between 10 and 20.

83002H
Q7: Sam types a constant number of words per minute.
He takes 8 minutes to type a report of 416 words.
How long does it take him to type an essay of 1534 words?
Give your answer in minutes and seconds.

83002H
Q8: A school play takes place each day from Monday to Friday.
Here are the attendances on four of the days.
Monday Tuesday Wednesday Thursday
72 83 88 97
For all five days, the mean attendance is 90
Work out the attendance on Friday.

83002H
Q9: Rosie makes phone calls to try to sell broadband.
Today, she made 120 calls.
The table shows the results.

Result of call Frequency
Not answered 33
Answered but sale not made 81
Answered and sale made 6
(a) Write down the relative frequency that a call was not answered.

83002H
Q11:A shape is made by joining a right-angled triangle to a rectangle.
Work out the area of the shape.

83002H
Q13: Outside a cafe there is a large plastic ice cream cornet.
The cornet is a hemisphere on top of a cone.

83002H
Q14: A survey was held in a football stadium.
A sample of the crowd was asked about the importance of a family area.
The pie chart represents the answers.

83002H
Q15: In the grid, the product of each row, column and diagonal is 1
Complete the grid.

83002H
Q16: Amol owns a sandwich shop.
The shop is open from Monday to Saturday.
In June, Amol sold 3000 sandwiches.
(a) Amol wants to work out the mean number of sandwiches he sold per day in June.
His method is 3000 ÷ 30 = 100
Make one criticism of Amol’s method.

83002H
Q20: A company makes and sells boxes of washing powder.
The company wants to increase the amount of money it receives per kg of powder.
To get the required increase it can
increase the price to £5.88
or
reduce the mass of powder in the box by x%
Work out the value of x to 2 decimal places.

83002H
Q24: A straight line
is perpendicular to the straight line through (2, 8) and (6, 15)
and
passes through (0, 9) and (x, 17)
Work out the value of x.

83002H
Q25: f(x) = 2x + 5
Show that 3f(x) – 12f^-1(x) simplifies to an integer

83002H
Q26: Two objects, J and K, are applying pressure to areas of ground.
For J, the force is 18.9 newtons and the area is 0.45 m2
pressure for J : pressure for K = 7 : 8
area for J : area for K = 9 : 5
Work out the force for K

83002H
Q27: To be rented, a bedroom must have a floor area of at least 6.51 m2
A bedroom has a rectangular floor.
The floor measures 2.4m by 2.9 m, each correct to 2 significant figures.
Show that the bedroom can be rented.

83002H
Q28: AB, BC and CD are sides of a regular 12-sided polygon.
CDMN is a square.
Prove that points A, B and N lie on a straight line.

83002H
Q29: The equation of a curve is y = x2 – 18x + 70
By completing the square, work out the coordinates of the turning point.
You must show your working.